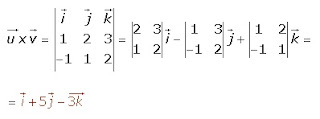Producto cruz
El producto cruz o producto vectorial de dos vectores es otro vector cuya dirección es perpendicular a los dos vectores y su sentido sería igual al avance de un sacacorchos al girar de u a v. Su módulo es igual a
El producto cruz se puede expresar mediante un determinante:
Ejemplos
Calcular el producto cruz de los vectores = (1, 2, 3) y = (−1, 1, 2).
Dados los vectores
hallar el producto cruz de dichos vectores. Comprobar que el vector hallado es ortogonal a U y v.
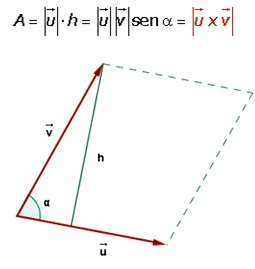
Área del paralelogramo
Geométricamente, el módulo del producto cruz de dos vectores coincide con el área del paralelogramo que tiene por lados a esos vectores.
Ejemplo
Dados los vectores
hallar el área del paralelogramo que tiene por lados los vectores U y v •
Área de un triángulo
Ejemplo
Determinar el área del triángulo cuyos vértices son los puntos A(1, 1, 3), B(2, −1, 5) y C(−3, 3, 1).
Propiedades del producto cruz
1. Anticonmutativa
2. Homogénea
3. Distributiva
4. El producto vectorial de dos vectores paralelos es igual al vector nulo.
5. El producto vectorial U x v es perpendicular a U y a v .